Homomorphic secret sharing
In cryptography, homomorphic secret sharing is a type of secret sharing algorithm in which the secret is encrypted via homomorphic encryption. A homomorphism is a transformation from one type of algebraic structure into another so that the structure is preserved. Importantly, this means that for every kind of manipulation of the original data, there is a corresponding manipulation of the transformed data.[1]
Contents[hide] |
Technique
Homomorphic secret sharing is used to transmit a secret to several recipients as follows:
- Transform the "secret" using a homomorphism. This often puts the secret into a form which is easy to manipulate or store. In particular, there may be a natural way to 'split' the new form as required by step (2).
- Split the transformed secret into several parts, one for each recipient. The secret must be split in such a way that it can only be recovered when all or most of the parts are combined. (See secret sharing)
- Distribute the parts of the secret to each of the recipients.
- Combine each of the recipients parts to recover the transformed secret, perhaps at a specified time.
- Reverse the homomorphism to recover the original secret.
Example: decentralized voting protocol
Shamir's secret sharing is a kind of homomorphic secret sharing in which a secret, represented by a number, is transformed into a polynomial. As a specific application, suppose a community is worried about corrupt authorities tampering with their votes. Instead of sending their votes to a single authority who might be corrupt, they decide to use secret sharing to distribute encrypted fragments of their votes to several authorities, hoping to decentralize the vote-counting process. In fact, Shamir's secret sharing has several advantages, which are discussed in more detail below. The protocol proceeds as follows:
Suppose that we have a simple ballot where a voter can either choose to vote yes (represented by the number +1) or no (represented by the number -1), and suppose there are  authorities who will be receiving the parts of votes.
authorities who will be receiving the parts of votes.
- Each voter generates a random polynomial of degree
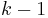 .
. 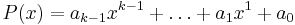 . The constant term
. The constant term 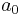 will equal the option they voted for, i.e.
will equal the option they voted for, i.e. 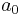 will be either +1 or -1.
will be either +1 or -1. - Each authority has a publicly-known ID number
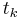 . Next, the voter calculates
. Next, the voter calculates 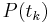 for each of the
for each of the  authorities. The
authorities. The 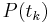 are the pieces of the secret, which are distributed to the corresponding
are the pieces of the secret, which are distributed to the corresponding  recipients along with their voter ID.
recipients along with their voter ID.
- The secret is secure because it takes
 points to recover a polynomial of degree
points to recover a polynomial of degree 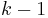 . (Two points determine a line, three points determine a parabola, and so on)
. (Two points determine a line, three points determine a parabola, and so on) - Since it is mathematically impossible to determine the voter's choice with only one piece of the secret, the voter ID doesn't have to be confidential.
- Additionally, this system resists tampering because no authority would be able to predict how altering their piece would affect the vote.
- The secret is secure because it takes
- After voting has been completed, each authority adds up the pieces he has received from all of the voters, and then sends this sum to the rest of the authorities.
- Recall that the secret has been transformed via
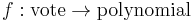 . Because
. Because  was a homomorphism, adding up the polynomials precisely corresponds to adding up the votes, that is
was a homomorphism, adding up the polynomials precisely corresponds to adding up the votes, that is 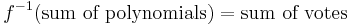 .
.
- Recall that the secret has been transformed via
- When the
 sums from the
sums from the  authorities are all known, the sum-polynomial
authorities are all known, the sum-polynomial 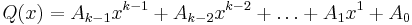 can be calculated.
can be calculated. 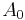 will be the sum of all the votes received. (Hence if
will be the sum of all the votes received. (Hence if 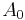 is positive, more votes were received for yes than no, and if
is positive, more votes were received for yes than no, and if 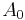 is negative, more votes were received for no than yes.)
is negative, more votes were received for no than yes.)
Features
This protocol works as long as not all of the  authorities are corrupt—if they were, then they could collaborate to reconstruct
authorities are corrupt—if they were, then they could collaborate to reconstruct 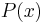 for each voter and then alter the votes.
for each voter and then alter the votes.
The protocol requires t+1 authorities to be completed, therefore in case there are N>t+1 authorities, N-t-1 authorities can be corrupted, which gives the protocol a certain degree of robustness.
The protocol manages the IDs of the voters (the IDs were submitted with the ballots) and therefore can verify that only legitimate voters have voted.
Under the assumptions on t:
- A ballot can not be backtracked to the ID so the privacy of the voters is preserved.
- A voter can not prove how he voted.
- It is impossible to verify a vote.
The protocol implicitly prevents corruption of ballots. This is because the authorities has no incentive to change the ballot since each authority has only a share of the ballot and has no knowledge how changing the ballot will affect the outcome.
Vulnerabilities
- The voter can not be certain that his vote had been recorded correctly.
- The authorities can not be sure the votes were legal and equal, for example the voter can choose a value which is not a valid option ( i.e. not in {-1, 1} ) such as -20, 50 which will tilt the results in his favor.
References
- ^ Schoenmakers, Berry (1999). Advances in Cryptology 1666: 148–164. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.102.9375&rep=rep1&type=pdf.
See also
- End-to-end auditable voting systems
- Electronic voting
- Certification of voting machines
- Techniques of potential election fraud through physical tampering with voting machines
- Preventing Election fraud: Testing and certification of electronic voting
- Vote counting system
- E-democracy
- Secure multi-party computation